Copulas made simple with Pytorch Distributions
Copulas in General
A copula is a mathematical tool for drawing correlated samples from high dimensional distributions, when you know a lot about the one-dimensional marginal probabilities for a few variables but not as much about the correlated samples.
For example, Suppose that you knew the returns of SPX on 4000 days and could construct a reasonable empirical distribution, and likewise the returns of VIX on 4000 days. However only 500 samples were joint samples on the same days. You would like the marginal distributions to have all the quality of the 4000 samples, but also like to train (by maximum likelihood) a correlated model. Copulas are the answer to this problem. They let you use your highly structured uni-variate marginal distributions with the correlation structure of another multivariate distribution.
The main ingredient in a copula is a parent correlated multivariate distribution, for example a multivariate Gaussian. Somewhat confusingly in the mathematical literature, the word copula is associated with the multivariate CDF of this parent distribution. You need to have access to the marginal CDF’s of this multivariate distribution and their inverses, call them: \(\phi_\text{MV}(x),\phi^{-1}_\text{MV}(x)\)
One builds a copula in a few steps:
- Construct your 1d marginal distributions for each series (\(\{ X_i, Y_i \}\)). (for example build the empirical cumulative distribution \(\phi_X(x) = \int_{-\infty}^x \rho_X(x) \approx \sum_i^n (x > X_i)/n\)
- Take the 500 good joint samples you have. Convert each into a sample of the uniform distribution \(\in [0,1]\) using the CDF of the X,Y distributions: \(\{ \phi_X(X_i), \phi_Y(Y_i) \}\).
- Now you have samples which are marginally uniform but correlated. Convert them into samples lying in the range of the multivariate distribution by applying the inverse cdf of the multivariate marginal. \(\{ \phi^{-1}_\text{MV}(\phi_X(X_i)), \phi^{-1}_\text{MV}(\phi_Y(Y_i)) \} = \{\tilde{X_i},\tilde{Y_i}\}\)
- Finally use Maximum Likelihood estimation to fix the parameters of the (unit variance) parent multi-variable distribution such that they likelihood of \(\{ \tilde{X_i},\tilde{Y_i} \}\).
Once such a model is obtained one can draw correlated multivariate samples from the copula by basically following these steps in reverse.
- Generate samples from the correlated multivariate.
- Map them back onto the uniform distribution using \(\phi_\text{MV}\) for each dimension.
- Use these correlated, but marginally-uniform samples with the inverse CDF of each dimension: \(\phi^{-1}_X, \phi^{-1}_Y \rightarrow \{ X_i , Y_i\}\)
Simple Gaussian Copula’s in Pytorch
Pytorch’s distribution’s module isn’t as well developed as Tensorflow’s or pyro, but I do find it more convenient to use.
def tch_cov(x, rowvar=False, bias=False, ddof=None, aweights=None):
"""Estimates covariance matrix like numpy.cov"""
# ensure at least 2D
if x.dim() == 1:
x = x.view(-1, 1)
# treat each column as a data point, each row as a variable
if rowvar and x.shape[0] != 1:
x = x.t()
if ddof is None:
if bias == 0:
ddof = 1
else:
ddof = 0
w = aweights
if w is not None:
if not tch.is_tensor(w):
w = tch.tensor(w, dtype=tch.double)
w_sum = tch.sum(w)
avg = tch.sum(x * (w/w_sum)[:,None], 0)
else:
avg = tch.mean(x, 0)
# Determine the normalization
if w is None:
fact = x.shape[0] - ddof
elif ddof == 0:
fact = w_sum
elif aweights is None:
fact = w_sum - ddof
else:
fact = w_sum - ddof * tch.sum(w * w) / w_sum
xm = x.sub(avg.expand_as(x))
if w is None:
X_T = xm.t()
else:
X_T = tch.mm(tch.diag(w), xm).t()
c = tch.mm(X_T, xm)
c = c / fact
return c.squeeze()
def mle_gaussian_copula(Fy, analytical = False):
"""
Finds a gaussian maximum likelihood copula.
To use this to draw correlated samples you feed in
1d-CDF values at empirical samples (Fy)
Then you sample the copula distribution,
feed that into the normal CDF, and then make the
result the unform noise for your derived samples ie:
C = mle_gaussian_copula(tch.tensor(fy))
U_samps = tch_normal_cdf(C.rsample(sample_shape=[20000]).detach().cpu()).numpy()
y_samp = np.stack([D_SPX.sample(ent = U_samps[:,0]),
D_VXX.sample(ent = U_samps[:,1]),
D_TLT.sample(ent = U_samps[:,2]),
D_GLD.sample(ent = U_samps[:,3]),
],-1)
Args:
Fy: marginal CDFs evaluated at y ie: F_{i}(y_i)
"""
tch.set_default_tensor_type('torch.DoubleTensor')
dim = Fy.shape[1]
n_corr = dim*(dim-1)//2
s_inds = tch.arange(dim)
t_inds = tch.tril_indices(dim, dim)
txs = t_inds[0].flatten()
tys = t_inds[1].flatten()
U = tch_normal_icdf(Fy.clamp(0.,1.))
std_t = U.std(0)
cov = tch_cov(U)/tch.einsum('i,j->ij',std_t,std_t)
print("Cov:", cov)
LL = tch.cholesky(cov + 0.001*tch.eye(dim))
if (analytical):
sigma0 = tch.matmul(LL,LL.permute(1,0))
print("Sigma0",sigma0)
sigma0[s_inds,s_inds] = tch.ones(dim)
L = tch.cholesky(sigma0)
return tch.distributions.MultivariateNormal(tch.zeros(dim),
scale_tril=L,
validate_args=None)
corrs = tch.nn.Parameter(LL[txs,tys], requires_grad=True)
params = [corrs]
optimizer = tch.optim.Adam(params, lr=2e-3)
def get_distribution():
L0 = tch.zeros([dim,dim])
L0[txs,tys] = corrs
Sigma0 = tch.matmul(L0,L0.permute(1,0))
Sigma0[s_inds,s_inds] = tch.ones(dim)
L = tch.cholesky(Sigma0)
D=tch.distributions.MultivariateNormal(tch.zeros(dim),
scale_tril=L,
validate_args=None)
return D
for step in range(10000):
optimizer.zero_grad()
D=get_distribution()
cy_term = D.log_prob(U)
loss = -1*cy_term.mean()
loss.backward()
tch.nn.utils.clip_grad_norm_(params, 7.)
optimizer.step()
if (step%100==0):
print("step {} loss {}".format(step, loss))
return get_distribution()
def tch_normal_cdf(Y):
return 0.5*(1.+tch.erf(Y/np.sqrt(2.)))
def tch_normal_icdf(Y):
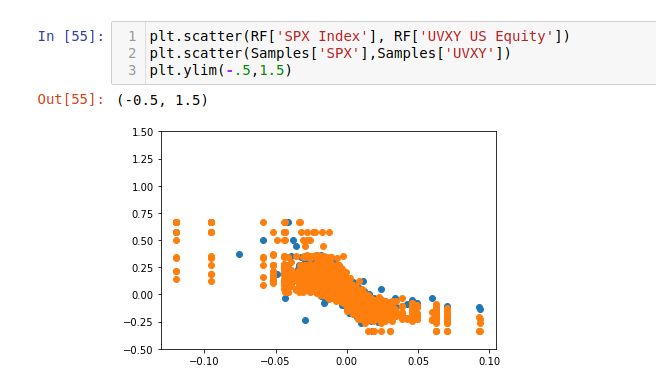
return np.sqrt(2.)*tch.erfinv((2.*Y-1.).clamp(-1+1e-13,1-1e-13))The image below compares samples from a copula constructed of SPX and UVXY returns, vs. samples of real returns from each asset.
Generalized Gumbel Copula.
A nice feature of maximum likelihood estimation is that when experimenting with different parent multivariates, you can always determine if your fit to the correlation structure of your data is better or not. As far as mathematics goes, copulas are young, and there isn’t a lot of data out there about what’s better or worse. There’s also a dearth of options beyond Gaussian. In my own research, I came across expressions for a copula built on the multivariate Gumbel distribution. Implementing this copula was a lot of work, although for my purposes it didn’t outperform the Gaussian distribution. I’m leaving this here in the hopes it might be of use to someone….
def gumbel_1d_cdf(samples, mu=0, beta = 1):
z = ((samples - mu)/beta).clamp(-12.,12.)
return tch.exp(-tch.exp((-1.*z)))
def gumbel_1d_pdm(samples, mu=0, beta = 1):
z = ((samples - mu)/beta).clamp(-12.,12.)
return tch.exp(-1.*(z + tch.exp(-1.*z)))/beta
def gumbel_1d_icdf(samples, mu=0, beta = 1):
return -beta*tch.log(-tch.log(samples))+mu
class GeneralizedStandardGumbel(tch.nn.Module):
def __init__(self, alpha, rho, thresh=1e-20):
"""
Implements a multivariate Gumbel with correlation alpha matrix.
alpha = upper triangular alpha matrix. all elements in (0,1)
rho = rho parameter \in (0,1)
"""
super(GeneralizedStandardGumbel, self).__init__()
self.dim = alpha.shape[0]
t_inds = tch.triu_indices(self.dim, self.dim, 1)
txs = t_inds[0].flatten()
tys = t_inds[1].flatten()
self.sftpls = tch.nn.Softplus()
self.alpha = tch.nn.Parameter(alpha[txs,tys])
self.rho = tch.nn.Parameter(rho*tch.ones(1))
self.n_pairs = self.dim*(self.dim-1)//2
self.thresh = 1e-14 # Used many places for numerical stability.
# These enforce the positivity constraints on the params
@property
def alpha_(self):
"""
The sum of coefficients for an index must be one.
I do that here recursively by normalizing the last "free" index
"""
a0 = self.sftpls(self.alpha)
t_inds = tch.triu_indices(self.dim, self.dim, 1)
txs = t_inds[0].flatten()
tys = t_inds[1].flatten()
alpha = tch.zeros(self.dim,self.dim)
alpha[txs,tys] = a0
alpha[0] /= alpha[0].sum()
for i in range(1,self.dim-1):
alpha[i] *= (1.-alpha[:i,i].sum())/(alpha[i].sum())
return alpha
@property
def rho_(self):
return (tch.tanh(self.rho)+1.)/2.
@property
def one_over_rho_(self):
return (1+tch.exp(-2.*self.rho))
def cdf(self, y):
"""
note: y must have dimension (1+sqrt(1+8*n_pairs))/2
"""
emy = tch.exp(-y).clamp(self.thresh,1e13)
# t1=tch.pow(tch.einsum('ij, ...i->...ij',self.alpha_, emy), 1./self.rho_)
# t2=tch.pow(tch.einsum('ij, ...j->...ij',self.alpha_, emy), 1./self.rho_)
if (y.dim() > 1):
alpha__ = self.alpha_.unsqueeze(0).repeat(y.shape[0],1,1)
t1a = tch.where(alpha__ >0, tch.einsum('...ij, ...i->...ij',alpha__, emy), tch.zeros_like(alpha__))
t2a = tch.where(alpha__ >0, tch.einsum('...ij, ...j->...ij',alpha__, emy), tch.zeros_like(alpha__))
t1=tch.pow(t1a.clamp(self.thresh,1./self.thresh), self.one_over_rho_)
t2=tch.pow(t2a.clamp(self.thresh,1./self.thresh), self.one_over_rho_)
else:
t1a = tch.where(self.alpha_ >0, tch.einsum('ij, i->ij',self.alpha_, emy), tch.zeros_like(self.alpha_))
t2a = tch.where(self.alpha_ >0, tch.einsum('ij, j->ij',self.alpha_, emy), tch.zeros_like(self.alpha_))
t1=tch.pow(t1a.clamp(self.thresh,1./self.thresh), self.one_over_rho_)
t2=tch.pow(t2a.clamp(self.thresh,1./self.thresh), self.one_over_rho_)
return tch.exp(-tch.pow((t1+t2).clamp(self.thresh,1./self.thresh), self.rho_).sum(-1).sum(-1)).clamp(self.thresh,1./self.thresh)
def pdf(self, y_):
"""
"""
ys = [y_[...,i].clone().detach().requires_grad_(True) for i in range(self.dim)]
Y = tch.stack(ys,-1)
Ps=[self.cdf(Y).sum()]
for i in range(self.dim):
Ps.append(tch.autograd.grad(outputs=Ps[-1].sum(), inputs=ys[i],
create_graph=True, retain_graph=True)[0].contiguous())
return Ps[-1]
def log_prob(self, y_):
return tch.log(self.pdf(y_)+self.thresh)
def rsample(self, nsamples=8000, batch_size=8000, M=400):
"""
Trivial Rejection Sampling.
"""
accepteds = []
sum_len_accepteds = 0
while sum_len_accepteds < nsamples:
proposal_D = tch.distributions.MultivariateNormal(tch.zeros(self.dim), scale_tril=tch.eye(self.dim))
proposal = proposal_D.rsample(sample_shape=[nsamples])
fx = M*tch.exp(proposal_D.log_prob(proposal))
g = self.pdf(proposal)
g_o_mf = g/fx
uniform = tch.ones(nsamples).uniform_()
accepted = proposal[tch.logical_and(g_o_mf > uniform , tch.logical_not(tch.isnan(g_o_mf).sum(-1)))]
accepteds.append(accepted)
sum_len_accepteds = sum(map(lambda X: X.shape[0],accepteds))
# print(sum_len_accepteds)
return tch.cat(accepteds,0)[:nsamples]
def mle_gumbel_copula(Fy_):
"""
The same as mle_gaussian_copula except with the
multivariate gumbel (fat correlations)
Args:
Fy_ : correlated samples of the marginal CDF's (ie: bw 0,1)
"""
tch.set_default_tensor_type('torch.DoubleTensor')
dim = Fy_.shape[1]
n_corr = dim*(dim-1)//2
t_inds = tch.triu_indices(dim, dim,1)
txs = t_inds[0].flatten()
tys = t_inds[1].flatten()
rho=0.01
alpha_ud=0.1*tch.ones(n_corr)
alpha = tch.zeros(dim,dim)
alpha[txs,tys] = alpha_ud
with tch.no_grad():
U = gumbel_1d_icdf(tch.tensor(Fy_).clamp(0.,1.))
U[tch.isinf(U)] = 0
U[tch.isnan(U)] = 0
D = GeneralizedStandardGumbel(alpha, rho)
optimizer = tch.optim.Adam(D.parameters(), lr=2e-3)
last_logprob = 0.
for step in range(10000):
optimizer.zero_grad()
cy_term = D.log_prob(U)
if (tch.any(tch.isnan(cy_term))):
print("Nan Loss ")
print(Fy[tch.isnan(cy_term)])
return None
loss = -1*cy_term.mean()
if (abs(last_logprob - loss) < 1e-5):
break
else:
last_logprob = loss.item()
loss.backward()
tch.nn.utils.clip_grad_norm_(D.parameters(), 7.)
optimizer.step()
if (step%100==0):
print("step {} loss {}".format(step, loss))
return D